Як дізналися висоту Евересту?

Згідно зі старою легендою, коли валлійський геодезист і географ сер Джордж Еверест виміряв висоту гори Джомолунгми, у нього вийшло рівно 29 000 футів у висоту (8839,2 метра), і його команда вирішила додати два фути до їх вимірювання, щоб зробити його більш правдоподібним. Стало вважатися, що хмарний гігант спокійно піднімається, відокремлений від решти, на висоті 29 002 футів над рівнем моря.

Згодом поява складних технологій, таких як супутники, оцінило висоту піку в 29 029 футів у висоту (8848,04 метра). Однак відкриття сера Евересту надзвичайно примітно, враховуючи, що він зробив це в 1852 році без допомоги інструментів, якими в даний час оснащені географи.

Більш того, його команда виконала вимірювання більш ніж в 100 милях від піку, оскільки уряд Непалу не дозволяло британцям в'їжджати в їхню країну. Отже, як вони досягли цього дивного вимірювання?

тригонометрія
У дитинстві найпростішим методом, щоб визначити довжину, було масштабування відстані рукою. Єдиною одиницею виміру було б відстань між великим пальцем і мізинцем, коли рука була помірно розтягнута.

Щоб виміряти, скажімо, стіл, потрібно було покласти на нього свою руку. Потім мізинець рухався вперед, дозволяючи великому пальцю зайняти своє місце, і так до тих пір, поки вся довжина була врахована.

Зрештою, руки були замінені лінійками, але методологія залишилася колишньою - складайте одну за з іншого, поки не буде покрита вся довжина. Ніхто не буде заперечувати, що вимір висоти Евересту з лінійкою, можливо, але всі погодяться з тим, що процес буде дуже трудомістким і громіздким.

Проте, метод, на який покладаються географи, недалекий від використання лінійок. Фактично, сер Еверест і його команда застосували шкільну геометрію для вимірювання висоти гори Еверест. Так, це вірно, тільки їх інструменти були просто більш химерними, більш складними наборами лінійок і транспортиров.

Тригонометрія була використана ще греками для вимірювання високих структур і вікторіанської геодезистами для вимірювання найвищих гір, перш ніж ми стали використовувати супутники. Однак навіть супутники вимірюють висоту, вони по суті реалізують той же принцип - малюють трикутники.

трикутники
Географи вимірюють висоту, малюючи численні трикутники. Серед трьох сторін, одна - це висота гори, яку потрібно виміряти. Підстава трикутника знаходиться між підставою гори і точкою, скажімо, яка розташована на відомій відстані від підставі гори. Третя сторона може бути сформована шляхом простого з'єднання точки А і вершини.

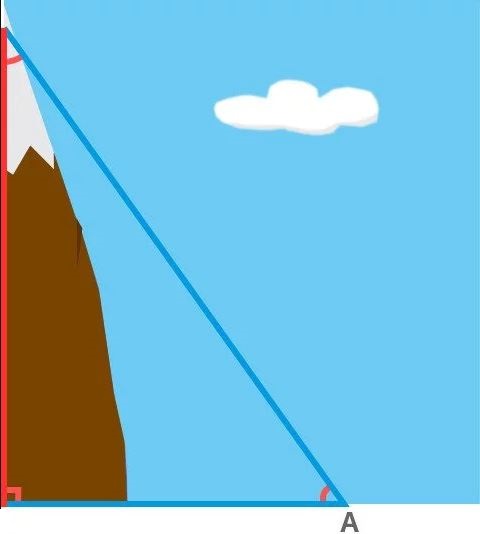
При формуванні горизонтального підстави географи повинні переконатися, що воно повністю вирівняно для досягнення точних результатів. Облік будь-яких нерівностей на поверхні Землі досягається за допомогою дуже тонких інструментів. Далі вони повинні виміряти всі три кути, утворені всередині трикутника. Це досягається шляхом використання попереднього транспортира, відомого як теодоліт. Вимірювання навіть двох кутів досить, так як третій кут може бути обчислений шляхом віднімання суми двох відомих кутів з 180 градусів, так як сума всіх трьох кутів, обмежених трикутником, дорівнює 180º.

Тепер ви можете зрозуміти магію простого тригонометричного дива - знання двох кутів і довжини одного боку може розкрити висоту гори. Навіть древні греки вимірювали висоту, «порівнюючи співвідношення двох сторін трикутника».

Наприклад, розглянемо дуже простий приклад, коли кут, утворений в точці А, дорівнює 60º, і ми знаємо тільки відстань між точкою А і підставою гори, яке, звичайно ж, є підставою трикутника. Для простоти припустимо, що трикутник прямокутний, де підставу перпендикулярно висоті. Це означає, що третій кут, сформований на вершині, становить 30º (180º- [90º + 60º]). Давайте також позначимо сторони трикутника. Починаючи з висоти і рухаючись за годинниковою стрілкою, позначимо їх як X, Y і Z.

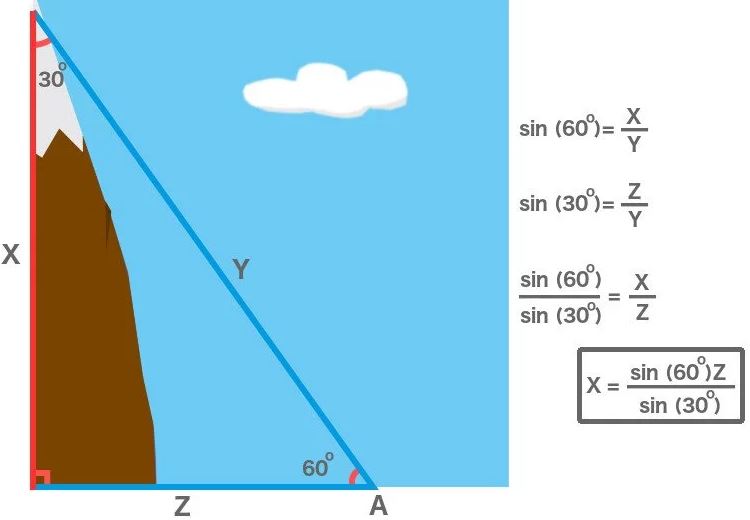
Тепер Синус Sin (60º) представляє відношення X / Y, тоді як синус Sin (30º) представляє відношення Z / Y. Якщо ми розділимо ці відносини, зауважимо, що два Y скасовуються, і ми залишаємося тільки зі ставленням X / Z. Значення обох синусів 60º і 30º можна дізнатися, просто звернувшись до підручника математики середньої школи. Крім того, Z є підставою трикутника, величину якого ми вже знаємо. Помножте Z з відносинами Синуса, і ми маємо висоту гори - X.

Джордж Еверест намалював кілька таких трикутників, все з різними відстанями А, оскільки вимірам одного трикутника можна довіряти. Потім команда усереднити кожну висоту, отриману з усіх трикутників. Це призвело до того, що вони отримали значення 29 000 футів, число, яке, за чутками, було збільшено, щоб уникнути будь-яких підозр.

Пізніше, в 1999 році, вчені за допомогою супутників виміряли висоту Евересту як 8848 метрів вище середнього рівня моря. Точність вимірювань Джоржа Евересту виявилася дивовижною - справжня висота піку виявилася найбільше на 8,23 метра, ніж він передбачив. Використовуючи тільки два кути і одну сторону!

Якщо ви знайшли помилку, будь ласка, виділіть фрагмент тексту і натисніть Ctrl + Enter.